Pressure, Atmosphere and Instrumentation
Pressure instruments are widely used in aviation. This article introduces the basic components of pressure as relevant to gliding. We shall then discuss how the pressure varies in the atmosphere, and the implications of this on the functioning of pressure instruments.
The author finds it very hard to discuss such topics without the aid of mathematical formulae. Every effort shall be made to explain the physical background of all the definitions and theorems used. If there is something you cannot understand, please consult an instructor who may determine what level of mathematical understanding (if any) is necessary. You do not need to be a physicist or engineer to fly gliders.
Contents
Fundamental Thermodynamics
Thermodynamics is a basic science that deals with energy. Its most notable application being the generation of power through heat engines. However, the only bit of thermodynamics we need to understand pressure is the Ideal Gas Law.
States and thermodynamic properties
Air can be liquified, but for all aviation purposes air is a gas. We shall not define a gas but the reader should have a good understanding of the concept through life experience.
Any substance of engineering interest can have states. For example, water can be ice, liquid water, or water vapour. If you are asked the question "What is the state of water at room temperature?" you may intuitively answer "liquid water". However, believe it or not, by reaching this conclusion you are making the assumption that the pressure that this water is at is at everyday atmospheric level. If the same water is put into vacuum while maintained at the same temperature, it will boil.
Therefore, to fully define the state that a substance is at, two thermodynamic properties must be specified. The most common thermodynamic properties can be:
- Temperature \(T\)
- Pressure \(p\)
- Density \( \rho \)
and a bunch of others. At least two must be known to fully define the state of a substance.
It is very important to understand that, by calling a thermodynamic property a property, it is implied that it belongs to the substance. It does not depend on the way you look at it, or, in physical language, it is independent of the frame of reference. For example, when you stand still you think the air is stationary at a temperature of 25°C, but if you drive past in a car you will think the air is moving. This does not, however, affect the fact that the air is still at 25°C. We shall see later that we can define some other things that depends on motion, known as the stagnation quantities, sometimes incorrectly referred to as "stagnation properties".
Ideal gas
Air can be modelled as an ideal gas. An ideal gas is a gas for which the following relationship holds:
\[ p = \rho R T \]
where:
- \(p\) is the pressure
- \(\rho\) is the density
- \(R\) is a constant that is a property of the gas itself, and
- \(T\) is the temperature.
Therefore, if we want to find the density of some air, both the pressure and the temperature needs to be specified (it is possible to substitute one or both with something else, but we shall not investigate this complexity). For example, atmospheric air and the air in a tyre are at the same temperature, but since the air in the tyre has a higher pressure (if you remember pumping it in), it has a higher density than atmospheric air.
In this equation, the temperature and pressure must be absolute quantities. In other words, the temperature (with the unit of Kelvins) needs to be measured against absolute zero (where the entropy of any perfect crystal is zero), and the pressure is measured against absolute vacuum (the pressure to be found in a finite volume in which there is no substance). You may have come across the term "gauge pressure" where the pressure is measured against something else: these relative quantities are incompatible with thermodynamics.
Pressure
Three types of pressure are used in the physics of flying. This section introduces the concepts, which will be used subsequently in later sections.
Pressure is a potential. It measures the ability of some gas to do useful mechanical work. Compressed gas can be used to move a piston and start an engine, for example, because that gas is at high pressure. Thus, a gas at some pressure also has some energy associated with it. Understanding this part will show that some definitions are not invented in random.
Definitions
Incompressible flow
A flow is incompressible if the fluid density does not change for the problem of interest. If a flow is incompressible, it does not imply that the fluid density cannot be changed in general. A flow that is not incompressible is compressible. We shall treat the air flow around a glider as incompressible: this is an assumption, but this can be justified by solving the compressible problem and show that the density change is absolutely tiny.
Static pressure
The static pressure, denoted as \(p\), is a thermodynamic property of the air. By the ideal gas Equation of State, the static pressure can be determined if the density and temperature are known.
Dynamic pressure
The dynamic pressure is a quantity (i.e. not a thermodynamic property) that describes the energy due to the motion of a fluid. If a body of mass \(m\) is moving at speed \(V\), then the kinetic energy it has is found to be:
\[E_K = \frac{1}{2} m V^2 \]
This can be shown by considering the work input to accelerate the body from rest to the speed \(V\).
We need something similar to describe the kinetic energy of a moving fluid, and we need this to have the dimensions of pressure. It is found that the following quantity is suitable:
\[p_D = \frac{1}{2} \rho V^2 \]
where \(p_D\) is defined as the dynamic pressure. It is the kinetic energy of one unit volume of fluid moving at the speed \(V\).
Total pressure
The total pressure, also known as the stagnation pressure, is a sum of the static and dynamic pressures.
\[ p_0=p+p_D \]
It is the static pressure that the fluid will reach if it is stagnated, i.e. brought to a rest from motion. If you stick an object into water flow (try this with a finger, be sure not to use hot water), you will observe the water level increase a bit in front of that object, which is a consequence of stagnating the water increasing its pressure, reflected in depth.
There is an extra requirement that the stagnation happens in an isentropic manner, but this is usually true when we consider air at low speeds. In fact, the stagnation of air is usually treated as isentropic unless we know it is not (for example, if we know a shock wave is present). Not being isentropic means mechanical energy is dissipated in the process, if you spill water on the ground and let itself come to a rest, you will not observe the level rise, for example.
Compressible effects
You may ask, if the static pressure is to increase, then by the ideal gas Equation of State, definitely the density and the temperature are to change? You are correct and this is the compressible effect which, up to now, the author has tried to avoid like the plague. Some people say that, because the flow is incompressible, the density remains constant and the temperature increases, but this is wrong because by invoking the Equation of State the assumption of incompressibility is voided automatically. In other words, the Equation of State has its foundation on the fact that gas molecules can get closer or further apart as governed by some rules.
What will happen is that the density and temperature will increase simultaneously. The precise amount we cannot solve for based on the equations presented in this article: other thermodynamic formulae relating temperature to pressure must be introduced. The exact solutions will be presented as a function of Mach number (the ratio between velocity and the local speed of sound).
Compressible effects get more obvious as the speed becomes higher. Back to the date when this was not well understood, quite a few aviation pioneers were killed by pushing the frontier of how fast we can fly. We should commemorate these sacrifices with great respect when we appreciate the great achievement the aviation industry has made to date.
If you are still interested, you may contact the author. You are encouraged to become an aeronautical engineer.
For the purposes of this article, forget about the Equation of State and assume that the density and temperature will remain constant when the flow is stagnated. If you cannot get your head around this, imagine we fly gliders in water. It can be shown that, for typical gliding speeds, the error introduced by ignoring the compressible effects are on the order of 0.1%.
Pressure coefficient
The pressure coefficient at point A (around an aeroplane), by definition, is:
\[ C_p(A) = \frac{p_A-p_{\infty}}{\frac{1}{2}\rho V_{\infty}^2} \]
where:
- \(p_A\) is the static pressure at point A
- \(p_{\infty}\) is the static pressure far away, and
- \(V_{\infty}\) is the flow velocity far away
By far away (known as free-stream quantities) we mean at a sufficient distance away from the aeroplane that effectively the flow is not disturbed by the aeroplane flying through it. Consider a car that passes in front of you at several feet away, you will feel some wind which is the flow disturbed by the presence of the car. However, you do not feel a lot of disturbance even if there are millions of cars driving in the United States.
Note that the velocity is measured in an aeroplane frame of reference so we can treat the problem as flow going around the aeroplane which makes things simpler. If the frame of reference is changed in this way, even the air above the United States can come at you at a velocity \(V\) depending on how fast you fly, so the author is just half joking when the above example is made.
The pressure coefficient is non-dimensional: it is a pressure divided by a pressure so no unit emerge from this algebra. However, if the flying speed is kept constant, i.e. the denominator is kept constant, the pressure coefficient is a representation of \(p_A\) given that the pressure in United States (\(p_{\infty}\)) does not depend on the way you fly. If \(C_p\) increases, it means \(p_A\) is higher.
The maximum possible value of \(C_p\) is unity, which corresponds to stagnating the flow. If all the kinetic energy has been transformed into pressure potential, there is nothing else whatsoever we can do to increase the flow pressure further (with the exception of adding some work by mechanical means, which we shall not consider). There is, in theory, no minimum value pf \(C_p\), so long as \(p_A\) is above zero.
How to measure pressure
A pitot tube is a device used to measure total pressure. It works by pointing a tube directly into flow so that the flow is brought to a rest when a bend or a capsule is reached (i.e. stagnated). As a result, the static pressure raises to the total pressure value of the free stream. A pitot tube is usually found at the nose of an aeroplane (e.g. the K-21s), but it can be elsewhere. There are designs where the pitot tube sticks out of the vertical stabliser (the fin) or on the side of the fuselage.
A static port is used to measure static pressure. This port must be located on an aeroplane where the pressure coefficient is zero. In addition, it needs to be perpendicular to the flow so that no dynamic pressure is converted into static pressure by the slowing down of the flow. On an aeroplane a static port (a small hole) is usually found on the side of the fuselage. You can ask an instructor to show you where this is.
The difference between the pitot tube reading and the static port reading is the dynamic pressure.
Note that there are restrictions on both of these regarding the relative direction with respect to the flow. The pitot tube and the static port are designed to function correctly when the aeroplane is flying unaccelerated with zero yaw and small angle of attack. If a significant amount of yaw is present, or if the angle of attack is extreme (such as when an aeroplane is stalled or flying inverted), these pressure readings will be unreliable. In case of intentional inverted flight, additional devices may be fitted to the pitot tube to improve the accuracy.
For reasons that should be obvious by now, it is important that the pitot tube and the static port are not blocked. This should be a part of the daily inspection of an aeroplane. Furthermore, there is a chance that the pitot tube may ice up in flight, for example, if the aeroplane is flown in rain at low temperatures.
Atmosphere
We rely on the atmosphere to survive, or, more importantly, to fly gliders. This section discusses some approaches to model the atmosphere and its properties at different altitudes. To be specific, we are interested in the static pressure distribution at different locations, which depends, according to the Equation of State, on the density and the temperature.
Simplified model
It is understood that a large pressure is present in the depth of the ocean. The same applies to the atmosphere: we are living at the bottom of an ocean of air.
Think about the ocean. You may know already from the science class that the water pressure comes from the weight of all the water above the location of interest. If you dive into the water you will feel the pressure, which originates as a result of a large amount of water directly on top of you resting its weight on you. Water pressure is given by (you will hopefully remember this from school):
\[p=\rho_{water} g H\]
Where \(g\) is the gravitational acceleration.
Air is not different. If we do the opposite and fly to high altitudes, because the amount of air resting on us is less (we have moved onto the top of a significant amount), the pressure will reduce. The formula to quantify this is:
\[p= p_{ground} -\rho_{air} g H\]
Where \(p_{ground}\) is the static pressure on the ground. This simple formula allows us to relate the decrease in static pressure to the altitude we are at, if we know the density of air and the gravitational acceleration (which we do). If we note down the ground pressure and continuously monitor the static pressure as we fly, it is possible to work out the altitude of the aeroplane. This is the fundamental principle of an altimeter.
Compressible effects
In the simplified model, it is assumed that the density of air is a constant. The Equation of State clearly says otherwise: density depends on pressure and pressure depends on density. Here we run into a problem and the problem can no longer be solved by simple algebra: the powerful mathematical tool of calculus must be used.
Even this is under the assumption that the temperature is a constant. The additional complexity is that the temperature in the atmosphere varies greatly, and you can feel this quite easily by climbing onto a hill and note the temperature drop (just make sure you use a thermometer instead of feeling, to isolate the effect of windchill). At low altitudes before the cloud base is reached, as a rule of thumb, the temperature will reduce by 3°C for every 1000 feet's rise of altitude. This is known as the dry adiabatic lapse rate.
The temperature of the air greatly depends on the heat transfer between the ground and the air: it is the ground that absorbs the radiation from the sun and heats up, the air is transparent so the absorptivity is quite low in the visible spectrum. Generally, the higher the altitude, the less heat the air will get from the ground, and, as a result, the air will become cooler. This applies until the tropopause is reached, beyond which the temperature ceases to decrease and, in fact, starts to increase again at higher altitudes. Gliders almost never reach the tropopause, so we can ignore this complexity.
This section sounds rather pessimistic, but the purpose is to demonstrate that there is no easy way to model the pressure and temperature distribution in the atmosphere accurately.
The International Standard Atmosphere
The International Standard Atmosphere (ISA) is a model for the atmosphere widely used in aviation. It is established based on extensive observations. It is not meant to be exact as the atmospheric conditions can vary actively (especially at low altitudes, known as weather). Also, the temperature in the atmosphere at low levels is subject to seasonality as we well understand. Despite these factors, the ISA is a good model and perhaps the most acceptable one to be used if some aviation equipment is to be designed.
The modelling approach of the ISA is to divide the atmosphere into several layers, within each layer the static temperature is assumed to vary linearly. If \(T\) is known, it is then possible to use the theories as described before to solve for the density and the static pressure simultaneously.
The ISA can come in a tabulated format with properties of the atmospheric air at discrete altitudes, or in an analytical format in which the mathematical solutions of the thermodynamic properties are presented as functions. These functions are piecewise, because the temperature function is so.
For aeroplanes that fly at high altitudes (especially above the tropopause), often an air data computer is carried on board, in which this model is coded for reference. For low level flying such as gliding, because the tropopause is not reached, the temperature is a linear function of altitude. Therefore, after some mathematical calculations, an explicit function mapping static pressure to altitude can be derived. This function is then implemented mechanically into an altimeter.
For the purpose of further discussions, it is important to understand that, for typical gliding altitudes:
- Temperature decreases linearly with altitude
- Static pressure decreases with altitude (according to a power law, though for gliding purposes this can be assumed to be linear)
- Density decreases with altitude
Instrumentation
This section describes the functions, working principles, and possible sources of error for pressure instruments that a pilot may wish to understand. Instrumentation is examinable in the Bronze theory examination, so the reader may wish to discuss the contents with an instructor to reinforce the understanding.
The usual pressure instruments used in gliding include:
- Air speed indicator (ASI)
- Altimeter
- Vertical speed indicator or Variometer
A glider is equipped to measure the following pressures:
- Total pressure, by using a pitot tube
- Static pressure, by using a static port
- Inverse pitot pressure, by using a total energy tube (see later)
Air speed indicator
An air speed indicator (ASI) is used to measure the airspeed of an aeroplane. The airspeed measured from an ASI is known as "indicated airspeed".
Airspeed vs. ground speed
Airspeed is the aeroplane's speed relative to the surrounding air (contrasted with ground speed, which is the speed relative to the ground). The reason airspeed can differ from ground speed is because the air itself can move, known as wind. If you fly at an airspeed of 40kts directly into a 40kts headwind, your ground speed will be zero, i.e. looking from the ground you will not be moving. This is because you move forward relative to the surrounding air, but the air is itself moving backwards relative to the ground, so the two effects cancel each other.
Function
The ASI is a pressure instrument, it works by measuring the total pressure and static pressure simultaneously. If you observe an ASI you will see it is plumbed both onto the pitot tube and the static port. An ASI is able to subtract these two readings, therefore, the dynamic pressure \(p_D\) can be obtained.
By using the formula introduced above, we obtain:
\[ V=\sqrt{\frac{2p_D}{\rho_{ASI}}} \]
If the density of the air is known. In an ASI, the density of air (\(\rho_{ASI}\)) is assumed to be a constant, and this constant is implemented mechanically into the architecture. The above formula is the definition of indicated airspeed, i.e. the airspeed that the ASI thinks the aeroplane is at.
Errors: TAS & IAS
Because the ASI assumes that the air density is a constant, if we fly under any condition where the actual density of air is not the same as the value used in the ASI (\(\rho_{air} \neq \rho_{ASI}\)), the airspeed that the ASI reads will not be the true airspeed (TAS). TAS is the airspeed of an aeroplane if examined in a kinematic sense, i.e. it will be the speed of the aeroplane you see if you remain stationary relative to the air.
Most of the times the instrument designers are not completely stupid, so the constant density hard coded into the ASI is not a random number. It is actually the average density of air at sea level, which the airfields and airports are usually not far away from. Therefore, at low levels where the density is quite close to the sea level density, the ASI is reasonably accurate. The problem most commonly arises when aeroplanes are flown at high altitudes: as we have discussed in the atmosphere section, the density of the air decreases with altitude. Therefore, the higher the altitude, the larger the difference between the IAS and the TAS. For example, a jet airliner that operates at FL360 can read an IAS of 280kts, but the TAS is actually around 450kts. For flying in wave lift which can take a glider to high altitudes, this is an important point to understand: you will travel faster than the ASI tells you.
A rule of thumb for calculating TAS corrections is, for every 1000ft above mean sea level, the TAS is 2% higher than the IAS. For example, if you fly at QNH 5000ft, your TAS will be 10% higher than your IAS.
Stall speed, performance airspeed and \(V_{NE}\)
Just like the altimeter, it is possible to correct for the density variations with altitude in an ASI, but this is not done for a very important reason: the stall speed (\(V_S\)).
An aeroplane stalls when a critical angle of attack is reached (See also: Aerofoils and Wings). There is a one to one mapping between the angle of attack (\(\alpha\)) and the lift coefficient (\(C_L\)), which is defined as:
\[C_L=\frac{L}{\frac{1}{2} \rho V^2 A} =f(\alpha)\]
Where:
- \(L\) is the lift force, equal to the weight of the aeroplane when flying unaccelerated
- \(A\) is the wing area, which is fixed unless devices such as flaps are in the process of deployment
- Note that \(\frac{1}{2} \rho V^2\) is the dynamic pressure
If the angle of attack is to reach a critical value, the lift coefficient is also to reach a critical value. Because the weight of the aeroplane (equal to the lift) and the size of the wings are fixed, we conclude that the aeroplane needs a minimum amount of dynamic pressure to fly: any less and the aeroplane stalls. This amount depends on the cockpit weight which is significant for a glider.
Recall that an ASI actually measures the dynamic pressure, so it can be used to indicate the point of stall, i.e. it is possible on each occasion to calculate the critical dynamic pressure and mark its value on the ASI. In practice the markings on the ASI are typically based on the maximum all-up weight.
We want this stall speed to be a well defined value that the pilot can easily compare a cockpit reading to. In other words, the stall speed should be a function of the critical dynamic pressure and nothing else. Therefore, the stall speed defined for an aeroplane is an indicated airspeed. If the ASI does not correct for the density variations and read the IAS all the time, the pilot can conveniently compare his flying to the stall speed. In other words, the ASI shows the stall margin correctly.
Note that the reasoning above applies to other flying conditions apart from stalling: the mapping between the angle of attack to a wide range of aerodynamic performances is one to one. Therefore, other speeds such as the speed of minimum sink (best glide) are also best defined as indicated airspeeds. In other words, the polar of the glider is invariant when expressed in terms of IAS. It, therefore, makes a lot of sense that the aeroplane keeps track of its indicated airspeed even if, with the aid of modern computers, calculating the TAS is a piece of cake. On larger aeroplanes with sophisticated avionics, the TAS is displayed real-time for navigational reference.
However, the never exceed speed (\(V_{NE}\)) has nothing to do with angle of attack or dynamic pressure: it is the speed that, when exceeded, the aeroplane may fail structurally. The failure of an airframe is dominated by aeroelastic effects, the most notable one being the flutter of the wings (there are videos on YouTube that shows this phenomenon). These horrible things occur when the TAS reaches a critical value. Recall that, at high altitudes, the TAS is higher than the IAS. Therefore, as you fly higher, your \(V_{NE}\), expressed in terms of IAS, will reduce. Failing to understand this can lead to serious consequences of overspeeding.
The point where the stall speed (IAS) corresponds to the never exceed speed (TAS) because of a decrease of density gives the theoretical ceiling. This is the theoretical maximum altitude at which the aeroplane can fly. If you fly at this altitude, you must fly at this speed precisely, or you will either stall or overspeed.
The Lockheed U-2, which flies at very high altitudes, have very notable problems when the ceiling is reached. For a U-2 in cruise, the difference between the stall speed and the never exceed speed is less than 10 knots apart on the ASI. This calls for very accurate handling by the pilot. The same applies to glider pilots who wish to fly at high altitudes: you must remember that the airspeed window in which you can fly is reduced, and, by flying higher, the red mark on the ASI must gradually move inwards. Such a feature is available on a jet airliner in the 1960s: there is a \(V_{NE}\) flag on the ASI which is driven by the air data computer.
Altimeter
An altimeter is an instrument that displays the vertical distance between the aeroplane and a reference datum, which is defined by the sub-scale setting on the altimeter.
An altimeter is a compensated instrument, which means the density variation in the atmosphere is automatically corrected for. An altimeter, therefore, gives reliable readings at all altitudes with the exception of readings very close to zero, in which regime the absolute errors become significant.
An altimeter needs to be read in the same way as a clock: ask an instructor to demonstrate this if you are not fluent at this. Altimeters come with 100ft and 1000ft hands, and most of them found in gliders also have 10000ft hands.
Setting
A datum level must be defined for the altimeter, and it is important to remember at all times that the altimeter reading is relative to the datum you the pilot have chosen. Depending on the situation in flight, the datum used may or may not be helpful.
Three settings are relevant to general aviation, they are QFE, QNH, and STD respectively.
QFE means the datum level is at airfield elevation. In this setting, the altimeter reads zero on the ground at the airfield where it flies from. In local circuit training and local soaring, the QFE is normally used. However, when the terrain surrounding the airfield is not level, the QFE setting does not guarantee a correct indication of the height above the ground. QFE is also useless if a circuit and land is planned at locations other than the home airfield, which is the reason you must be comfortable to circuit and land without reference to the altimeter. In addition, if a very long soaring flight is being made, the QFE levels at the take off time and the landing time can be different.
QNH means the datum level is at the mean sea level. This is a useful setting for cross country flights, because all the altitude values given on a chart are above mean sea level (with some exceptions such as obstacles above the ground, in which case a height above the ground is also quoted). It is possible to circuit, approach and land with QNH, which power pilots do (their standard instrumental terminal procedures involve checkpoints with altitudes prescribed in QNH), but the usefulness is limited in gliding as all operations are supposed to be under visual flight rules, and visual approaches rely little on knowing the absolute height above the ground.
STD is the setting where the sub-scale is adjusted to 1013hpa or 29.92in Hg. This setting shows flight levels. For example, FL55 is 5500ft when the altimeter is at the STD setting. This is useful if navigating at great altitudes or if attempting to avoid airspace.
Vertical speed indicator (power)
A vertical speed indicator is a differential instrument: it works by differentiating the static pressure to obtain the rate of climb or descent. In particular, the following relationship holds:
\[ V_S= -\frac{1}{\rho g} \frac{dp}{dt} \]
A vertical speed indicator uses the static port pressure as an input, and uses mechanical methods to differentiate it with respect to time (via the use of a calibrated leak or other means, or electronically). A vertical speed indicator (or "uncompensated variometer") is rarely used in gliding because it is not able to show the increase or decrease of the total energy which is more important than the absolute climb or descent, as glider pilots frequently trade height for speed and the other way. If you trade your speed for altitude a vertical speed indicator will show that you are climbing, but in fact you are losing total energy slightly, as gliders do so often that it has got its own name "stick thermal". For this reason, a vertical speed indicator is not particularly good in the identification of lift sources in soaring.
A vertical speed indicator is important for power aeroplanes as they are usually required to maintain altitude, and this instrument responds faster then an altimeter for the pilot to take correction actions. Furthermore, in the planning of vertical navigation for power aeroplanes, being able to know the vertical speed is useful.
Total energy in gliding: a more interesting quantity
What a glider pilot is more interested in is the total mechanical energy of a glider, which has two components: the gravitational potential energy (altitude), and the kinetic energy (speed).
In a mathematical form, this can be expressed as:
\[E = E_P + E_K = mgH + \frac{1}{2} m V^2 \]
Where:
- \(m\) is the mass of the glider, which does not change very often in flight
- \(g\) is the gravitational acceleration, a constant
- \(H\) is your altitude
- \(V\) is your speed
For the simplicity of the following discussions, we shall assume that a glider flies in dead still air, so we can avoid the problem of defining the frame of reference for the speed: the true airspeed and the ground speed are the same. Furthermore, we shall assume that the glider manoeuvres in such a small altitude range that the density of air can be treated as a constant \(\rho\).
Consider a glider which has descended from \(H_1\) to \(H_2\), in which process its velocity has increased from \(V_1\) to \(V_2\). We shall, for the purpose of the discussion, assume that the glider has not lost any mechanical energy during the process, i.e. the glider experiences zero drag (!)
The mechanical energy is conserved, therefore:
\[ E_1 = E_2\]
\[ mgH_1 + \frac{1}{2} m V_1^2 = mgH_2 + \frac{1}{2} m V_2^2\]
Rearranging the above equation, we cancel the mass terms and obtain the following relationship:
\[ V_2^2 - V_1^2 = 2g \times (H_1-H_2) \]
Note that the sign conventions are correct: \(V_2>V_1\) while \(H_1>H_2\).
Now suppose there is a mysterious instrument "Anyometer" on the aeroplane that is a pressure instrument. The Anyometer uses a pressure source at location X on the aeroplane as its input. Suppose that, at location X, the pressure coefficient is \(C_{pX}\). By rearranging the definition presented before, we have the following relationships:
\[ p_{X1}=p_1+C_{pX} \frac{1}{2} \rho V_1^2 \]
\[ p_{X2}=p_1+C_{pX} \frac{1}{2} \rho V_2^2 \]
Now the Anyometer is designed so that, when the aeroplane descends from \(H_1\) to \(H_2\) as outlined above, its reading does not change, in other words:
\[ p_{X1} = p_{X2} \]
Substituting the two equations for \(p_{X1}\) and \(p_{X2}\) and rearranging slightly, we have:
\[ p_1 - p_2 = C_{pX} \times \frac{1}{2} \rho (V_2^2 - V_1^2) \]
Where \(p_1-p_2\) is the static (atmospheric) pressure difference at \(H_1\) and \(H_2\) respectively. Because \(H_2\) is lower than \(H_1\), \(p_2\) is higher than \(p_1\). Explicitly, the following relationship from hydrostatics holds:
\[ p_1 - p_2 = -\rho g (H_1 - H_2) \]
Therefore:
\[ -\rho g (H_1 - H_2) = C_{pX} \times \frac{1}{2} \rho (V_2^2 - V_1^2) \]
We now substitute in the relationship \(V_2^2 - V_1^2 = 2g \times (H_1-H_2)\) as derived before, and everything will just cancel out magically. What is left is:
\[ C_{pX} = -1 \]
This is a remarkable result. This implies that if we can monitor the pressure at a location X on the aeroplane such that \( C_{pX} = -1 \), we can track the total mechanical energy change of the aeroplane. This is the fundamental working principle of a "total energy compensated variometer". When a "variometer" is installed on a glider, it usually refers to a compensated instrument as described above, although other types of compensation that shows other quantities of interest are available.
How to measure total energy
As outlined above, the problem of total energy compensation boils down to the problem of finding a location on the aeroplane where the pressure coefficient is -1. This is, however, not easy. We can get around this problem by designing a device which produces this pressure coefficient, just like a pitot tube is designed to produce a pressure coefficient of +1. This device is known as a total energy tube or total energy probe. There are mainly two kinds of architectures: the Venturi type (found on HTV) and the cylindrical type (found on KFY, JEC, PZ, and some other gliders at GRL).
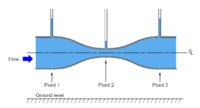
On the right is a schematic drawing of a Venturi tube[1]. In order not to bore the reader, the detailed mathematics is not shown here, but for this to work, the required area ratio is:
\[ \frac{A_2}{A_1} = \frac{1}{\sqrt{2}} \]
Measuring the pressure at point 1 (\(p_1\)) and point 2 (\(p_2\)) and subtract them, \(p_2-p_1\) gives a pressure coefficient of -1. In reality, the area ratio needs to be slightly different to correct for viscous effects which is not included in the derivation. A variant of this type of total energy tube, namely the Orifice type, is also suitable and probably easier to manufacture.
The drawback of a Venturi in measuring the total energy is that it is not tolerant to yaw. Most of the time when the total energy will be of interest is when the glider is soaring, and continuous turning is usually included in this process. If the glider has some yaw, the air will not enter the Venturi in the correct direction but it needs to turn a bit. This changes the pressure in the Venturi and leads to unreliable readings. A more benign design is the cylinder type.
A schematic drawing of a cylindrical type of total energy tube is also presented[2]. These resemble closely the total energy tubes found on gliders today. The working principle of these tubes is not trivial and a theoretical approach to the design of these is not available to the author's knowledge. Qualitatively, these rely on the low pressure found in the wake behind the cylinder created by the separation of the boundary layer. In 1976 NASA did extensive experiments on these devices and the optimal geometry was found and presented in the Technical Memorandum X-73928[3].
Variometer (gliders)
You hopefully have realised from the discussions above that a variometer on a glider is not different from a vertical speed indicator on a powered aeroplane. Indeed, the instrument themselves are identical, the only difference is that a gliding variometer has its input connected to the total energy probe. In this way, the variometer tracks the change of the total energy of a glider rather than the change of altitude solely. "Stick thermals" are thus suppressed and a reliable indication of the natural lift in the atmosphere becomes available.
On a glider, normally two variometers are fitted. There is a mechanical one and an electronic one. The mechanical one does not require battery power to function, so it is operational even if the battery goes flat, which is a possibility in a very long decent soaring day. The disadvantages being:
- A mechanical variometer is usually quite sluggish in its response: it can take several seconds before the actual change of trend is accurately displayed, during which time there is a good chance that the glider has flown beyond the best bit of a thermal.
- You need to actually look at the variometer to get a reading. While this is not a huge problem in normal flight because most of the instruments you have to look at to read, due to the special interest of the variometer reading in a soaring flight, pilots can very easily get so distracted that their lookout significantly deteriorates.
It is not acceptable under any circumstance (with perhaps the exception of flying under IFR, which a glider does not normally do) to cease to look out properly and direct too much attention on the instruments, otherwise the flying safety is at stake. To help the glider pilots to read the variometer without directing the attention to the panel, electronic variometers can be introduced. These are more responsive and they sound an audible tone whose pitch depends on the variometer reading. Normally a continuous tone indicates the total energy is decreasing, while a discontinuous beep means the total energy is increasing.